Here’s my solution to the Leetcode 315: Count of Smaller Numbers After
Self problem using standard merge sort. I just change one line to
count while merge procedure.
Solution#
Let’s build the solution step by step.
Input: nums = $$[5,2,6,1]$$
First, turn the numbers into [number, index] tuple. So it looks like:
array = $$ [ [ 5, 0 ], [ 2, 1 ], [ 6, 2 ], [ 1, 3 ] ] $$
Second, just write standard merge sort algorithm and sort the array in ascending order by first values.
The output is: $$ [ [ 1, 3 ], [ 2, 1 ], [ 5, 0 ], [ 6, 2 ] ] $$
Here’s the trace of the algorithm:
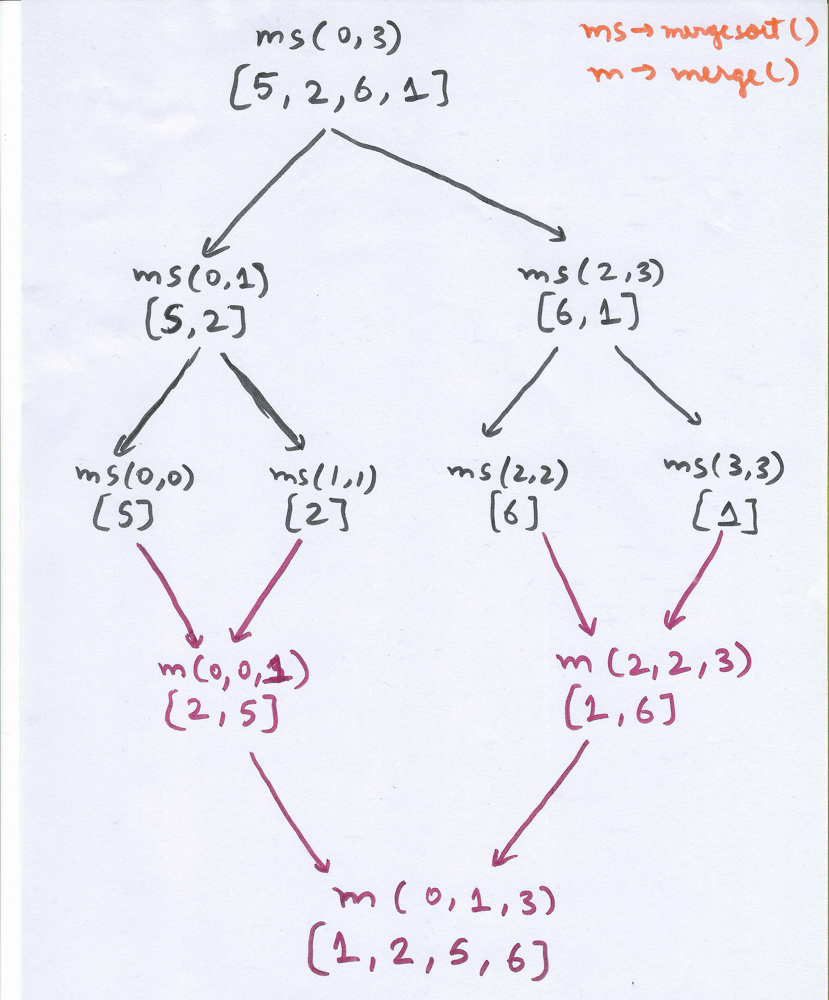
Simple merge sort implemented#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| const merge_sort = ( a, i, j ) => {
if ( i === j ) return;
const mid = i + Math.floor( (j-i)/2 );
merge_sort( a, i, mid );
merge_sort( a, mid+1, j );
merge( a, i, mid, j );
};
const merge = (a, start, mid, end) => {
const tmp = [];
let i = start, j = mid+1;
while ( i <= mid && j <= end ) {
if ( a[i][0] > a[j][0] ) {
tmp.push( a[j] );
j++;
}
else {
tmp.push( a[i] );
i++;
}
}
while ( i <= mid ) { tmp.push( a[i] ); i++; }
while ( j <= end ) { tmp.push( a[j] ); j++; }
for ( let i=0; i < tmp.length; i++ )
a[start+i] = tmp[i];
};
var countSmaller = function( nums ) {
const array = nums.map( (val, ind) => [val, ind] );
merge_sort( array, 0, array.length-1 );
};
|
So far so good.
Now let’s get back to the question. The question is asking:
For each index $$i$$, count all numbers at index $$j$$ such that $$i < j$$ and $$a[i] > a[j]$$. Or, simply put: for each number, find all numbers that appear after it and are smaller than it.
Now, look at the visualization again, pay attention to the merge procedure (in magenta colour) and observe the following:
- at each merge procedure, we merge 2 consecutive partitions.
- all numbers in the left partition appear before numbers in right partition in the original array.
- The partitions are sorted in increasing order.
Now, suppose we are merging 2 partitions where, the pointer of left partition is at $$x$$ and pointer of right partition is at $$y$$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| [....a,b,c, x ,d,e,f....] [...h,i,j, y, k,l,m....]
^ ^
i j
Suppose x > y
It follows from observation 2 that:
y is one of the numbers that appear to the right of x
and is smaller than x ---(1)
Also, since partitions are sorted (observation 3):
d, e, f .... (i.e. all number that appear to the right of x)
are greater than x. ----(2)
From (1) and (2) we can conclude that:
x, d, e, f, ... (i.e. all numbers to the right of x including x)
appear before y. And y is smaller than all these numbers.
Hence, required condition satisfied!
|
Now, we just need a counter for each variable, and whenever the condition same as above occurs, we increment the counter for each x,d,e,…
1
2
3
4
5
6
7
| [....a,b,c, x ,d,e,f....] [...h,i,j, y, k,l,m....]
^ ^
i j
while merging:
if x > y
increment the counters of x, d, e, f, ...
|
Single line changed in standard merge sort algorithm#
We can use the index at the second position to access the counter of that particular number.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| let counts;
const merge_sort = ( a, i, j ) => {
if ( i === j ) return;
const mid = i + Math.floor( (j-i)/2 );
merge_sort( a, i, mid );
merge_sort( a, mid+1, j );
merge( a, i, mid, j );
};
const merge = (a, start, mid, end) => {
const tmp = [];
let i = start, j = mid+1;
while ( i <= mid && j <= end ) {
if ( a[i][0] > a[j][0] ) {
/* ____(x > y) so increment counters of x,d,e,...____*/
for ( let p=i; p<=mid; p++ ) counts[ a[p][1] ]++;
/*_______________INSERT THIS LINE_____________________*/
tmp.push( a[j] );
j++;
}
else {
tmp.push( a[i] );
i++;
}
}
while ( i <= mid ) { tmp.push( a[i] ); i++; }
while ( j <= end ) { tmp.push( a[j] ); j++; }
for ( let i=0; i < tmp.length; i++ )
a[start+i] = tmp[i];
};
var countSmaller = function( nums ) {
const array = nums.map( (val, ind) => [val, ind] );
counts = new Array(nums.length).fill(0);
merge_sort( array, 0, array.length-1 );
return counts;
};
|
That is the whole idea behind this question. Now the above implementation won’t work because at each iteration, we are updating whole left partition after i. Making it O(n^2)#
Optimize#
To avoid updating the whole partition, we keep a running counter cnt.
Final implementation#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| let counts;
const merge_sort = ( a, i, j ) => {
if ( i === j ) return;
const mid = i + Math.floor( (j-i)/2 );
merge_sort( a, i, mid );
merge_sort( a, mid+1, j );
merge( a, i, mid, j );
};
const merge = (a, start, mid, end) => {
const tmp = [];
let i = start, j = mid+1;
let cnt = 0; // keep running counter
while ( i <= mid && j <= end ) {
if ( a[i][0] > a[j][0] ) {
cnt++; // increment counter
tmp.push( a[j] );
j++;
}
else {
counts[ a[i][1] ] += cnt; // no more numbers that are
// smaller than i
tmp.push( a[i] );
i++;
}
}
while ( i <= mid ) {
counts[ a[i][1] ] += cnt; // if left partition is not over
// update left over number counts
tmp.push( a[i] );
i++;
}
while ( j <= end ) { tmp.push( a[j] ); j++; }
for ( let i=0; i < tmp.length; i++ )
a[start+i] = tmp[i];
};
var countSmaller = function( nums ) {
const array = nums.map( (val, ind) => [val, ind] );
counts = nums; counts.fill(0);
merge_sort( array, 0, array.length-1 );
return counts;
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| def countSmaller(nums):
counts = [0] * len(nums)
array = [(num, i) for i, num in enumerate(nums)]
def merge_sort(start, end):
if start == end:
return
mid = (start + end) // 2
merge_sort(start, mid)
merge_sort(mid + 1, end)
merge(start, mid, end)
def merge(start, mid, end):
temp = []
i, j = start, mid + 1
cnt = 0
while i <= mid and j <= end:
if array[i][0] > array[j][0]:
cnt += 1
temp.append(array[j])
j += 1
else:
counts[array[i][1]] += cnt
temp.append(array[i])
i += 1
while i <= mid:
counts[array[i][1]] += cnt
temp.append(array[i])
i += 1
while j <= end:
temp.append(array[j])
j += 1
for i in range(len(temp)):
array[start + i] = temp[i]
merge_sort(0, len(nums) - 1)
return counts
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| #include <vector>
using namespace std;
vector<int> countSmaller(vector<int>& nums) {
vector<int> counts(nums.size(), 0);
vector<pair<int, int>> array;
for (int i = 0; i < nums.size(); i++) {
array.emplace_back(nums[i], i);
}
function<void(int, int)> merge_sort = [&](int start, int end) {
if (start == end) return;
int mid = start + (end - start) / 2;
merge_sort(start, mid);
merge_sort(mid + 1, end);
merge(start, mid, end);
};
function<void(int, int, int)> merge = [&](int start, int mid, int end) {
vector<pair<int, int>> temp;
int i = start, j = mid + 1;
int cnt = 0;
while (i <= mid && j <= end) {
if (array[i].first > array[j].first) {
cnt++;
temp.push_back(array[j]);
j++;
} else {
counts[array[i].second] += cnt;
temp.push_back(array[i]);
i++;
}
}
while (i <= mid) {
counts[array[i].second] += cnt;
temp.push_back(array[i]);
i++;
}
while (j <= end) {
temp.push_back(array[j]);
j++;
}
for (int k = 0; k < temp.size(); k++) {
array[start + k] = temp[k];
}
};
merge_sort(0, nums.size() - 1);
return counts;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| import java.util.*;
class Solution {
private int[] counts;
private int[][] array;
public List<Integer> countSmaller(int[] nums) {
counts = new int[nums.length];
array = new int[nums.length][2];
for (int i = 0; i < nums.length; i++) {
array[i][0] = nums[i];
array[i][1] = i;
}
mergeSort(0, nums.length - 1);
List<Integer> result = new ArrayList<>();
for (int count : counts) {
result.add(count);
}
return result;
}
private void mergeSort(int start, int end) {
if (start == end) return;
int mid = start + (end - start) / 2;
mergeSort(start, mid);
mergeSort(mid + 1, end);
merge(start, mid, end);
}
private void merge(int start, int mid, int end) {
List<int[]> temp = new ArrayList<>();
int i = start, j = mid + 1;
int cnt = 0;
while (i <= mid && j <= end) {
if (array[i][0] > array[j][0]) {
cnt++;
temp.add(array[j]);
j++;
} else {
counts[array[i][1]] += cnt;
temp.add(array[i]);
i++;
}
}
while (i <= mid) {
counts[array[i][1]] += cnt;
temp.add(array[i]);
i++;
}
while (j <= end) {
temp.add(array[j]);
j++;
}
for (int k = 0; k < temp.size(); k++) {
array[start + k] = temp.get(k);
}
}
}
|
- Time: $$O(n\ log\ n)$$
- Space: $$O(n)$$
