Leetcode 715. Range Module is one of the most convoluted problems on leetcode. And your confidence is further shattered when you find out, that it can be solved in just 6 lines of code. Upon seeing these 6 lines, you realize that this is nothing less than a rosetta stone. In this blog post, I will run the code through all possible edge cases by hand.

Range Module

A Range Module is a data structure that tracks intervals of numbers using half-open ranges [left, right). It supports adding, querying, and removing ranges efficiently.

Problem Statement

Implement the RangeModule class with the following methods:

• addRange(left, right): Adds the interval [left, right), merging overlapping ranges if needed.
• queryRange(left, right): Returns true if every number in [left, right) is currently tracked.
• removeRange(left, right): Stops tracking all numbers in [left, right).

Example

1
2
3
4
5
6

rangeModule = RangeModule()
rangeModule.addRange(10, 20)
rangeModule.removeRange(14, 16)
print(rangeModule.queryRange(10, 14))  # True
print(rangeModule.queryRange(13, 15))  # False
print(rangeModule.queryRange(16, 17))  # True

You might want to come back to these definitions as you read through the solution:

1
2
3
4
5

bisect_left(a, x)
    The return value i is such that all e in a[:i] have e < x
    and all e in a[i:] have e >= x. So if x already appears in
    the list, a.insert(i, x) will insert just before the leftmost 
    x already there.

1
2
3
4
5

bisect_right(a, x) 
    The return value i is such that all e in a[:i] have e <= x
    and all e in a[i:] have e > x. So if x already appears in
    the list, a.insert(i, x) will insert just after the rightmost 
    x already there.

Insertion algorithm

Suppose (x, y) is the new interval. First we find

start pointer = s = bisect_left of x = and end pointer = e = bisect_right of y

The reason for this will be clear in a moment. First, we will consider movement of x only while keeping y fixed.

Case 1: New interval overlaps with some intervals inside

Now suppose, (x,y) do not overlap with any intervals on their ends, however, they contain multiple intervals inside of them. See below:

This applies while b < x <= c.

In this case, we can remove all the intervals that are contained inside (x,y) and replace all of them with just one interval i.e. (x, y). Here’s how the array looks after adding interval (x,y).

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 6  )
>>> s
2
>>> e = bisect_right( a, 27 )
>>> e
8
>>> a[2: 8] = [ 6, 27 ]
>>> a
[1,4, 6,27, 30,40]

Case 2: x = start of some interval

This is just a subcase of case 1. I am using it to show why we are using bisect_left for x.

The bisect_left on x will still provide us with s=2. Hence, we can still follow the same approach.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 7 )
>>> s
2
>>> e = bisect_right( a, 27  )
>>> e
8
>>> a[2:8] = [7, 27]
>>> a
[1,4, 7,27, 30,40]

Case 3: x intercepts some interval

In this case, the interval (x,y) intersects some interval on the left side i.e. c < x <= d for some interval (c, d) in (x, y). See below:

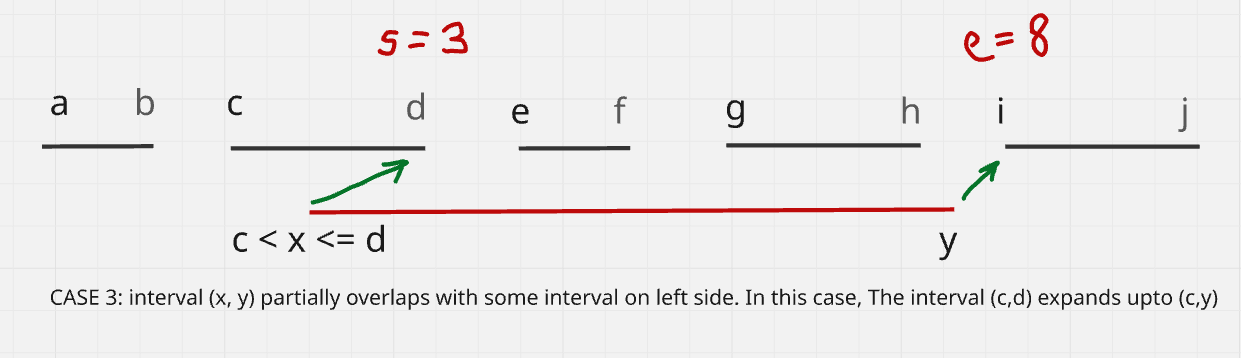
In this case, we can expand the interval (c, d) -> (c, y). Note that we do not need to remove c this time. We just need to add y as an ending. Hence, we basically remove all numbers in [s..e) and add y in their place.

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 8 )
>>> s
3
>>> e = bisect_right( a, 27 )
>>> e
8
>>> a[ 3:8 ] = [ 27 ]   # do not add left since s = some interval ending
>>> a
[1, 4, 7, 27, 30, 40]

If we move x further to the right (d < x). We basically arrive at case1 again with different intervals. So, now let’s try moving y around.

Case 4: y = ending of some interval

Suppose, we make y coincide with h. Hence, we get a situation where, y=ending of the last interval in (x,y). And note carefully here, that:

e = bisect_right(y) = i != h, because bisect right is exclusive

This is why bisect_right is required for y.

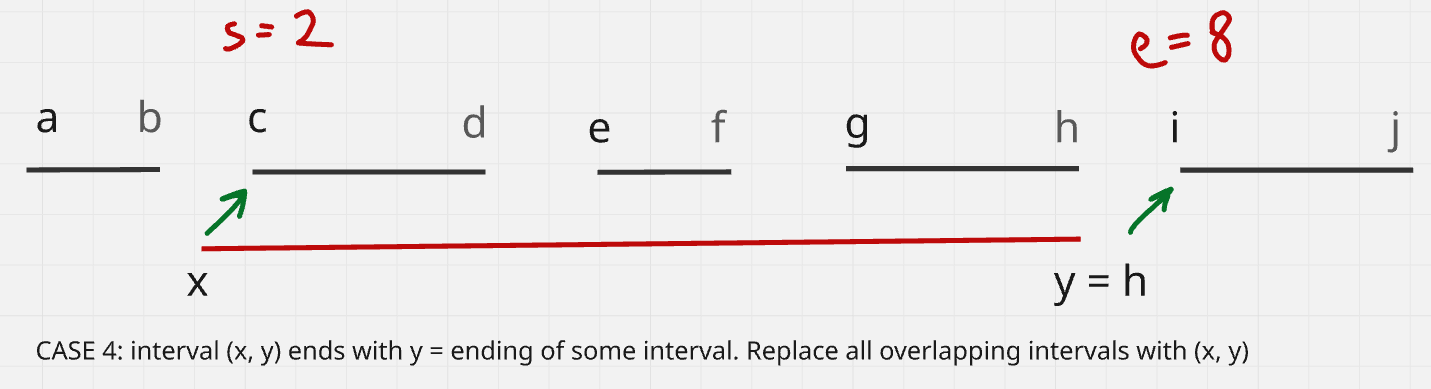
In this situation we will follow the same approach as in case1 i.e. remove all intervals and replace with (x,y).

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 6 )
>>> s
2
>>> e = bisect_right( a, 25 )
>>> e
8
>>> a[s:e] = [6,25]
>>> a
[1,4, 6,25, 30,40]

Case 5: y intercepts some interval

If y overlaps with the last interval on the right side. We need to expand (x, y) -> (x, h). As shown below:

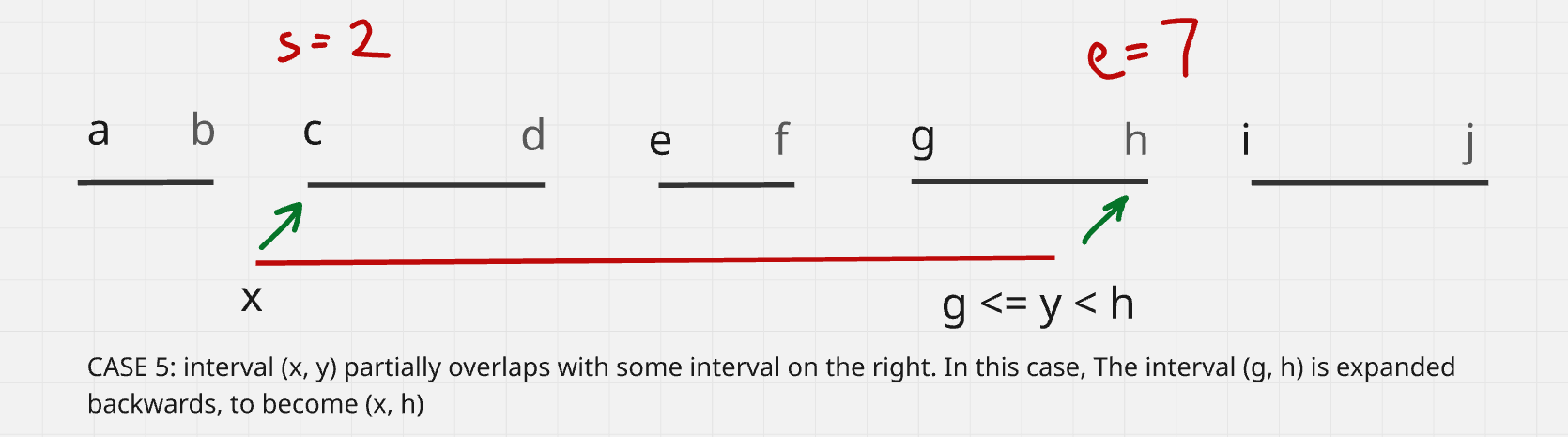
We are basically just removing all numbers in [s..e) and adding x in their place.

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 6 )
>>> s
2
>>> e = bisect_right( a, 23 )
>>> e
7
>>> a[2:7] = [ 6 ] # do not add y since, e points to end of some interval
>>> a
[1,4, 6,25, 30,40]

If we decrease y further to y < g then we end up in the same situation as case1. Hence, we’ve covered all cases. Let’s generalize our approach:

1
2
3

s, e = bisect_left(left), bisect_right(right)
a[s:e] =   [left]  iff s does not point to end of some interval
         + [right] iff e does not point to end of some interval

By now it should be clear that even indices represent start of intervals and odd indices represent end of intervals.

Case 6: What if there are no intervals or new interval does not overlap with any interval

This is an important edge case to consider. If there are no intervals, or (x,y) do not contain any intervals, then s,e will point to the same location, as shown below.

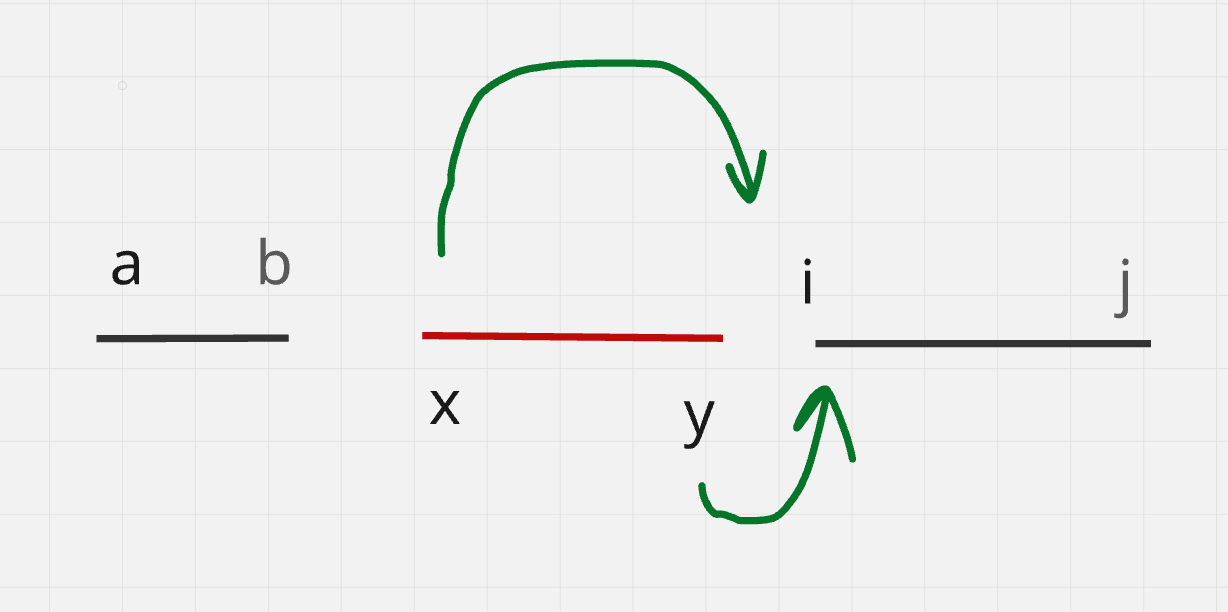
With a[x:x] = [left, right] python will insert [left, right] at index x. So it does not cause any problem:

1
2
3
4
5
6

>>> a = []
>>> s = bisect_left( a, 3 )
>>> e = bisect_right( a, 7 )
>>> a[s:e] = [3] + [7] # s=e=0 here
>>> a
[3, 7]

Removal algorithm

Case 1: Deletion interval overlaps with some intervals inside

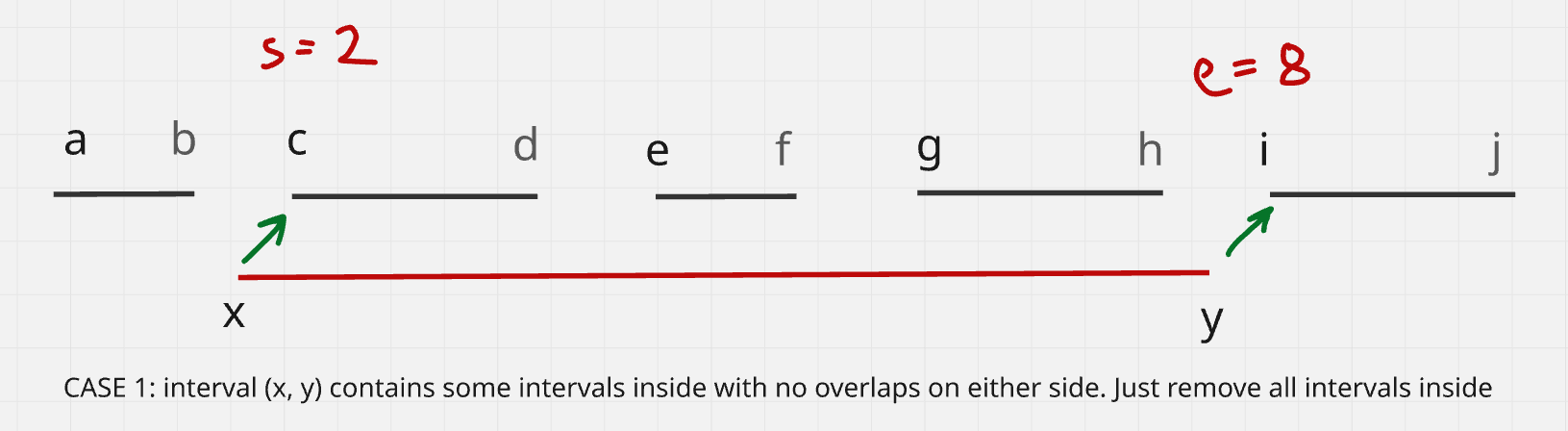
In this case, we should remove all intervals inside (x, y) as shown below:

Here, we are just remove all numbesr in [s..e).

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 6 )
>>> s
2
>>> e = bisect_right( a, 27 )
>>> e
8
>>> a[s:e] = [] # add nothing
>>> a
[1,4, 30,40]

Case 2: x intercepts some interval

If (x, y) overlaps with some interval on the left. We need to trim that interval. For example, suppose, (x,y) intercepts some interval (c, d). See below:

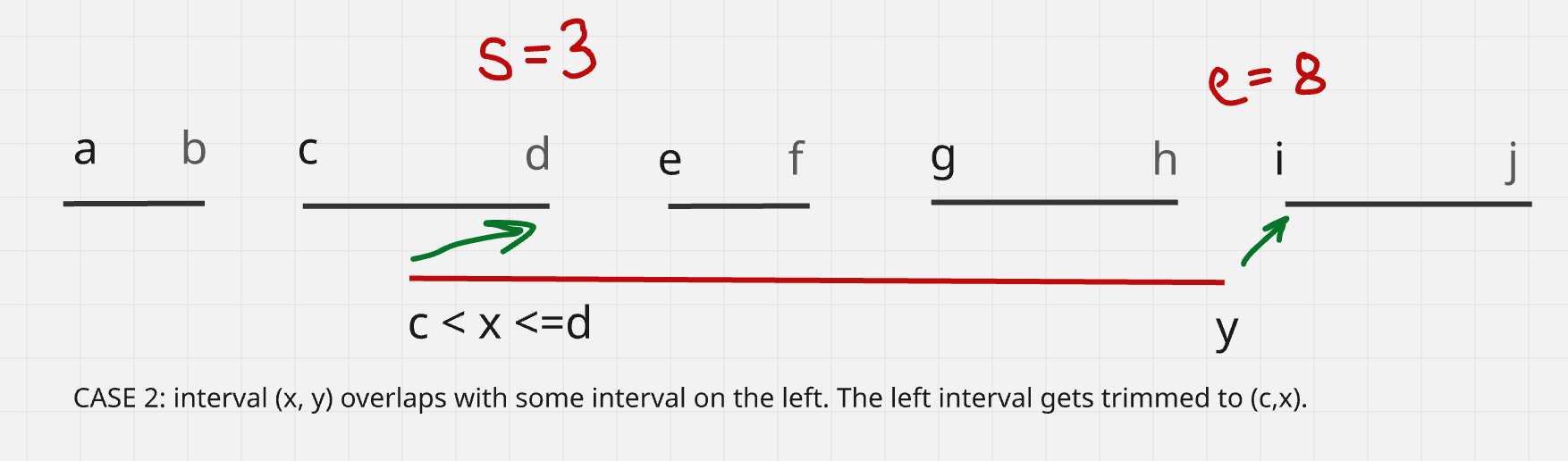
In this case we trim (c, d) -> (c, x). As shown below:

Basically, we remove all numbers in [s..e) and add x in their place.

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 8 )
>>> s
3
>>> e = bisect_right( a, 27 )
>>> e
8
>>> a[3:8] = [ 8 ] 
>>> a
[1,4, 7,8, 30,40]

Case 3: y intercepts some interval

Suppose (x, y) overlaps with some interval (g, h) on the right. See below:

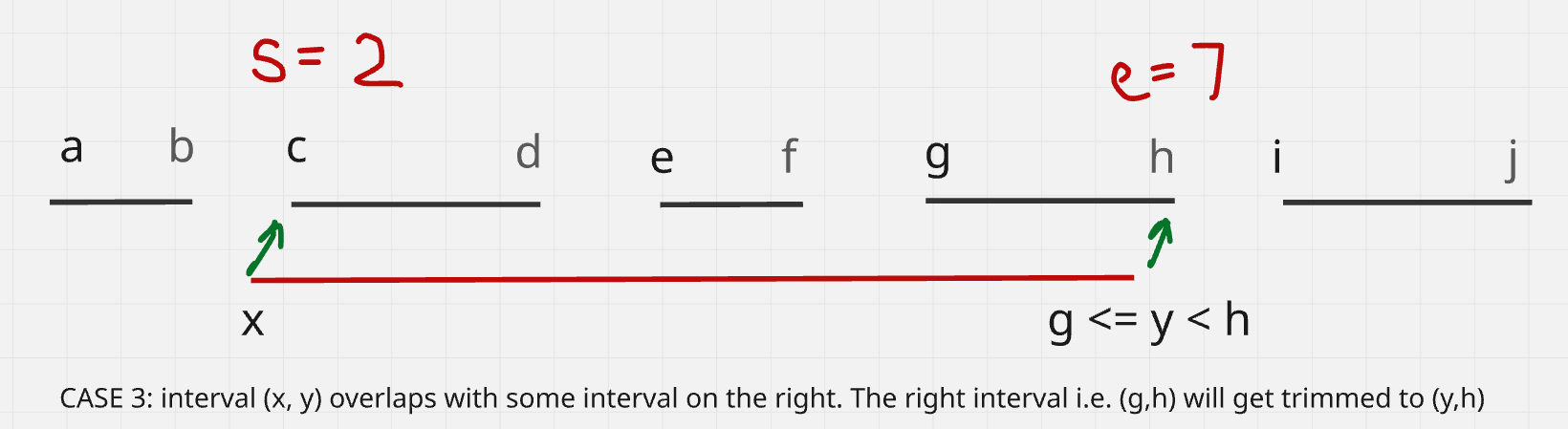
In this case, we need to trim the interval (g, h) -> (y, h). Here, we delete all numbers in [s..e) and insert y in their place.

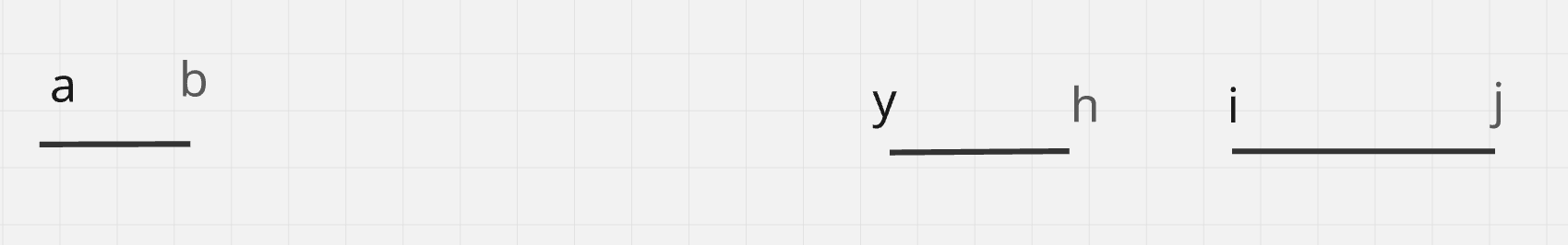
Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 6 )
>>> s
2
>>> e = bisect_right( a, 23 ) 
>>> e
7
>>> a[2:7] = [ 23 ] # add y
>>> a
[1, 4, 23, 25, 30, 40]

Case 4: (x, y) overlap with some intervals on both sides

If (x, y) intercepts some interval no both sides as shown below:

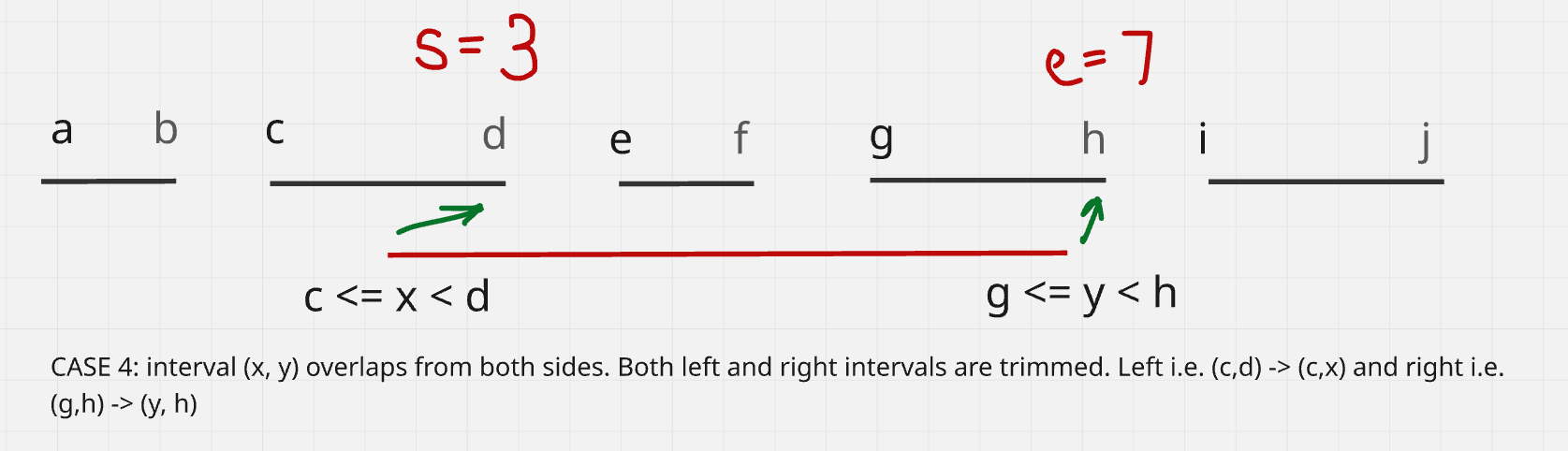
We need to trim both the affected intervals. For example if x intercepts (c,d) on the left. Then (c, d) is trimmed to (c, x). Similarly, if (g,h) is intercepted by y. We trim (g, h) to (g, y).

Note that we are just removing all digits in [s..e) and adding x,y in their place.

Sample:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

>>> a = [1,4, 7,10, 13,17, 20,25, 30,40]
>>> s = bisect_left( a, 8 )
>>> s
3
>>> e = bisect_right( a, 35 )
>>> e
9
>>> a[3:9] = [ 8 ] + [ 35 ]
>>> a
[1,4, 7,8, 35,40]

Hence, can generalize our approach as follows:

1
2
3

s, e = bisect_left(left), bisect_right(right)
a[s:e] =   [left]  iff s points to end of some interval
         + [right] iff e points to end of some interval

Searching algorithm

There is only one way for a range (x, y) to be tracked i.e. it MUST lie in one of the range intervals being tracked.

Consider the case, where (c, d) is a range currently being tracked. If (x, y) lie inside (c, d) then:

next of x = s = bisect_right(x) = d next of y = e = bisect_left(y) = d

Notice the use of bisect_right for x this time. This is because, @x=c we cannot return s=c.

Similarly, y uses bisect_left now. This is because, @y=d we cannot return i.

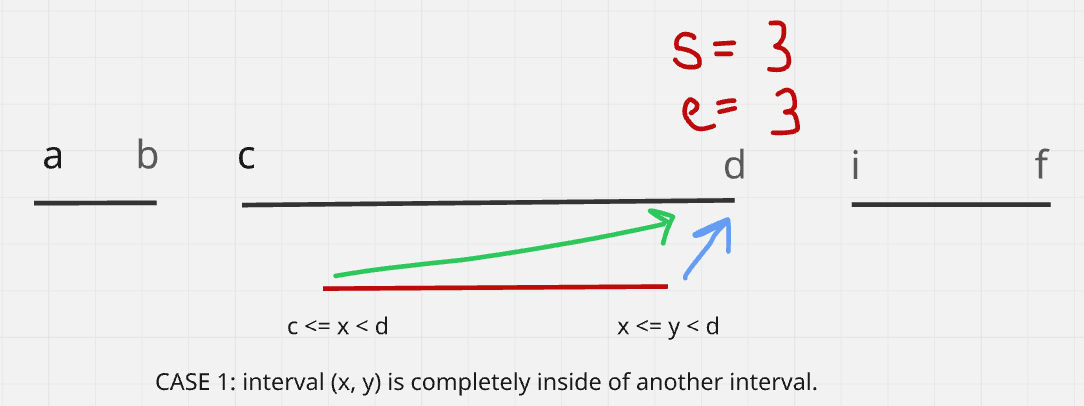
Both s and e must point to a single location which is ending of the current interval i.e. d.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

    def __init__(self): self.a = []

    def addRange(self, left, right):
        s, e = bisect_left(self.a, left), bisect_right(self.a, right)
        self.a[s:e] = [left] * int(s%2!=1) + [right] * int(e%2!=1)

    def queryRange(self, left, right):
        s, e = bisect_right(self.a, left), bisect_left(self.a, right)
        return s==e and s%2==1        

    def removeRange(self, left, right):
        s, e = bisect_left(self.a, left), bisect_right(self.a, right)
        self.a[s:e] = [left] * int(s%2==1) + [right] * int(e%2==1)