Leetcode 769: Max chunks to make sorted solution

When numbers from $$\in$$ [0,n-1] are sorted in an array of size n. Their sorted position is equal to their index.

Subset of numbers in array[i:j] can form a partition, if all elements in [i,j) are available in array[i:j].

For example [2,0,1] can form a partition, since they are at index 0, 1, 2 respectively. Sorted will involving swapping them at their correct position.

The basic idea behind this solution is that we try to identify such partitions, where all elements required to be sorted in [i, j] are available in current partition.

Here’s the visualization of the algorithm, i points to the start of the group and j iterates through the group and checks if the current group needs to be expanded. e points to the end of the current group.

Since, array[j]=1, we found a number greater than current boundaries. We need to expand the boundary. Hence, new group end is e = array[j].

Increment j. We find that array[1] = 0 which is < current end. Increment j again, j=2, Hence, no we exhaust the current group and we move forward to finding the next partition. Increase, current group ending, and reinitialize i=e/

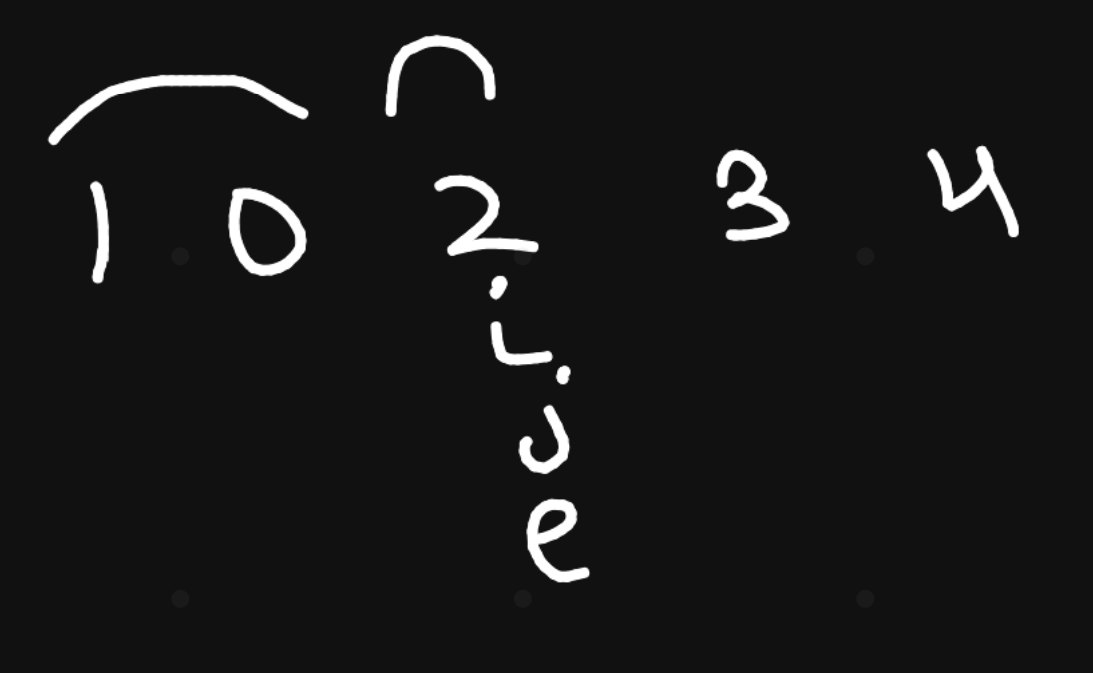
In the second group, we have array[j]=2 and we are at index 2. Hence, we do not need to expand this group, since 2 is at right position.

Similarly we find the next 2 partitions.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

int maxChunksToSorted(int* arr, int arrSize) 
{
    int cur_gp_end = 0, cnt_gps = 0, i = 0;
    while ( i < arrSize ) {
        int j = i;
        // try to terminate the current group
        while ( j <= cur_gp_end ) {
            cur_gp_end = fmax( cur_gp_end, arr[j] );
            j++;
        }
        i = ++cur_gp_end;
        cnt_gps++;
    }
    return cnt_gps;
}