Leetcode 775: Global and local inversions solution

When nums[i] > nums[j], it is global inversion. Local inversion is special case of global inversion with j=i+1

Consider the array: [0,1,2,3,4,5]

If i swap a random element by 2 positions (either to left or right). I will always create 2 inversions.

Likewise, if I swap a random element by 3 positions. I end up creating 3 inversions.

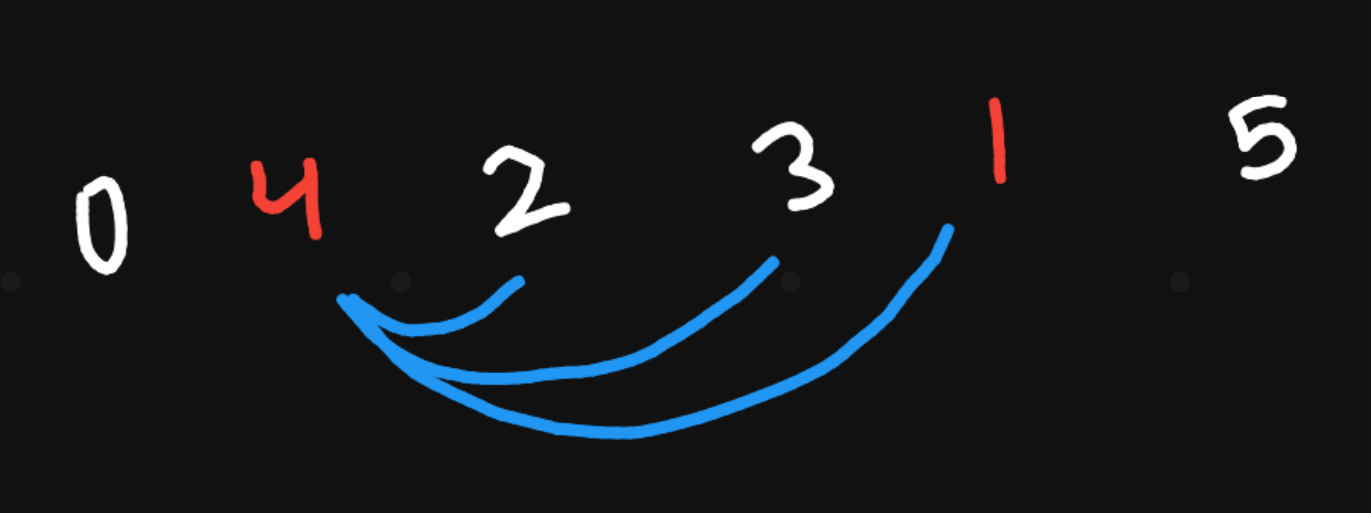
Similarly if I swap an element by 4 positions. I end up creating 4 inversions.

Note that for each swap made above, we created a single local inversion. This means that whever we swap 2 elements, we end up creating 1 local inversion and k global inversions. Where k means element swapped k number of positions away.

Now, we need number of local inversions = number of global inversions. This can only happen when local inversion is itself the global inversion.

Hence, for each swap we should only create 1 inversion, THEREFORE K=1

1
2
3
4
5
6
7
8

bool isIdealPermutation(int* nums, int numsSize) 
{
    for (int i=0; i < numsSize; i++) {
        if ( abs(nums[i]-i) > 1 ) 
            return false; 
    }
    return true;
}